How rainbows work!

[Isaac]

Introduction

In this guide we will be exploring the geometrical opitcs perspective of rainbows! This is an optical phenomenon that many of us have seen and appreciated for its aesthetic beauty and hopefully this guide will deepen that sense of amazement at the natural world and its majesty!

This guide was inspired by Walter Lewin (MIT professor who wrote, “The Love of Physics”) and his lectures on the topic. For more amazing content, see this youtube channel dedicated to preserving his lectures.

Background

To begin to understand the physics of how we see a rainbow, we need to lay down some ground work and a set of basic observations about rainbows from which to draw our conclusions. They are:

• Rainbows require a relatively uniform distribution of water droplets in the sky
• The sun’s rays (light) need an unobstructed path to the water droplets
• Primary (and secondary) rainbows are only seen when the sun is behind the viewer
• The arc of the rainbow traces out a cone angle of approximately 42 degrees
• The sun is far enough away that we can assume that all of the rays from the sun that hit the water droplets are parallel to each other (collimated).
• The index of refraction of water at the three primary colors is: n_{red} \approx 1.331, n_{green} \approx 1.336, and n_{blue} \approx 1.343.

For reference, an image of the phenomenon is included below. Source

Discussion

The questions we are going to answer in this guide are:

• If the sun is behind the you when you observe a rainbow, how does the light reach your eyes?
• Why is the rainbow in an arc?
• Why is the rainbow brighter in the center?
• Why are the bands of color only observed at the edge of the arc?
• Why is red on the outside and blue on this inside?

Before reading further, spend some time thinking about these questions on your own! Form your own hypothesis and test how they compare to the following conclusions.

We will start with a picture of a single water droplet. It is approximately spherical in shape and composed of primarily water.

We also draw a dashed axis through the water droplet that corresponds to the direction of the sun’s rays incident on the droplet. Note that this is not the observation direction.

The sun’s rays that are incident on the water droplet undergo refraction, obeying Snell’s Law, which states that

n_1 \sin \theta_1 = n_2 \sin \theta_2.

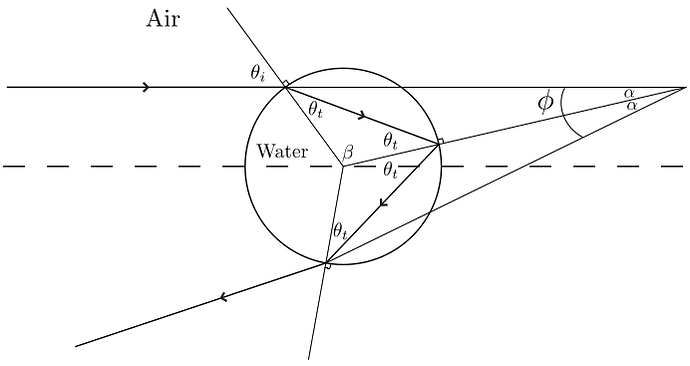
If we use the labels i and t to denote the incident and transmitted directions, respectively, we can build up a picture of how the ray travels through the droplet as shown below.

The fletching on the lines denotes the direction of the ray. We can see that the ray enters the droplet, bends towards the surface normal since it is encountering a larger index of refraction, travels through the droplet to the back surface and then does something unusual!

Instead of refracting, as we might expect, the ray reflects on the back surface of the water droplet! This phenomena occurs whenever we have a change in the refractive index, or at the boundary between two media. Camera lenses and other imaging devices try to reduce this effect using anti-reflective (AR) coatings. In truth, most of the light does refract again, exiting the back of the droplet and continues to travel in that direction. However, the smaller amount of light that reaches our eyes to form the rainbow reflects.

This light undergoes another reflection/refraction, but we are concerned with the refraction since it is returned towards the observer.

Given the path of the ray, we can label the picture with the angles \theta_i, \theta_t, \alpha, \beta, and \phi. \theta_i and \theta_t are the angles of incidence and transmittance, respectively which are carried through the droplet. \alpha and \beta are angles used to help determine the total deviation \phi of the ray. If we apply knowledge of geometry we find that

\alpha + \beta + \theta_i = 180,\\ \phi = 4\theta_t - 2\theta_i.

This expression of the total deviation has a maximum value as a function of incidence angle given by

\cos \theta_i^{max} = \sqrt \frac{n^2 - 1}{3},

which allows us to see why a rainbow forms an arc at approximately 42 degrees and has a bright band of colors!

If we input the indices of refraction that were given above for the three primary colors, we find that for red: \theta_i^{max} = 59.53 and \phi^{max} = 42.37 degrees, green: \theta_i^{max} = 59.24 and \phi^{max} = 41.64 degrees, and blue: \theta_i^{max} = 58.33 and \phi^{max} = 40.65.

These maximum angles correspond to the brightest band of each color, and since they occur at different angles, we see a dispersed spectrum of colors, forming the bands of the rainbow. Red on the outside since its maximum occurs at the largest angle, and blue on the inside.

Within the central region of the rainbow, the light returned from the droplets is mixed but does not have the same maximum, which means we see white light. This is in contrast to the outer section of the rainbow, which does not have the same amount of light being returned, and appears darker.

Conclusion

We have just begun to brush the surface of how rainbows work from a geometrical perspective. There are other effects like a supernumerary rainbow that require an understanding of diffraction (waves).

If you have any questions or comments leave them below in a reply! Thanks, and that’s all for this one.

Make Waves!