1. Frequency Domain
Often times in performing analysis on optical data, it can be useful to analyze your data set(s) in the frequency domain. Let me give one specific example that comes up relatively often. An optical surface is measured using some metrology method, lets say interferometry, to better understand the surface quality, and what impact that has on your system. However, the raw data obtained from a standard interferometry measurement device typically outputs a surface profile map. While this can be useful, and can reveal roughness and height imperfections, perhaps we need to go deeper to understand exactly what distribution those height imperfections are at; i.e. is the surface dominated by large, slowly changing shapes such as defocus and astigmatism (low frequencies) or rapidly changing surface roughness (high frequencies)?
I already somewhat gave it away in that last paragraph that we can draw a direct analogy of the surface shapes to a frequency analysis. Before I get to the analysis however, why is it important? If we do analyze our surface and discover it is dominated say by defocus for example instead of high frequency surface roughness issues, then we can easily compensate the error by simply adjusting the axial position of our optic. Or, lets say instead of something as simple as defocus, it is a combination of coma and astigmatism, still in the low frequency range. Again, we can perform mechanical adjustments to compensate, or can plate compensating optical components. However, if we find that the surface error is instead dominated not by low frequencies, but by high frequency errors, we don’t have many options besides additional surface polishing to correct for the issue. Thus, by analyzing the surface profile in the frequency domain we can better guide a fabrication process or a system level analysis! Of course, there are other areas of optics besides metrology that frequency analysis is required including but not limited to: laser systems, image analysis, sensing, and more. So the question becomes, if its so useful, how do I do it? Well, lets get to it!
2. Fourier Transform
Before we fully get into it, I want to say that my primary source for all things Fourier Transform related was Dr. Scott Tyo’s Opti 512R course from the University of Arizona. While he is no longer teaching the course there unfortunately, you can still find his course notes and recorded lectures on iTunes [1].
Now, I am not going to spend a lot of time describing the theory of a Fourier Transform or Fourier Series; suffice to say the Fourier Transform (FT) is a way to transform a periodic function into a weighted sum of sine and cosine terms. While it is not the only method of representing a function or data, it is one method which has excellent applicability to electrical and optical systems. For the interested reader, there are a variety of sources on the internet that discuss Fourier series in more detail [1,2,3].
Given an arbitrary complex valued function f(x), we define it’s Fourier Transform F(\xi) as:
We recognize that x and \xi are the FT variables, and have inverse units. For example, if x is given in length, \xi is in 1/length.
However, we are concerned with analyzing discrete digital data. In this scenario, we are analyzing discrete, periodic data, which implies that our Fourier Transform will similarly be discrete and periodic. To achieve this, we must perform the Discrete Fourier Transform (DFT).
3. Discrete Fourier Transform
Suppose our function is f(x) = 0 outside of the interval 0 \le x < L; and we have N equally spaced samples in this interval. This implies:
From the Whittaker-Shannon sampling theorem [4,5], given that our function f(x) is space limited, we know we can reconstruct (\xi) from samples taken at n \Delta \xi, as long as:
Therefore, we define our minimum sampling frequency as \frac{1}{\Delta\xi}. We can then sample our discrete space Fourier Transform as:
With eq. 5 giving the DFT of our discrete data. The inverse DFT (IDFT) is given as:
Before we move on to the actual algorithms for implementing the DFT, I want to highlight some important characteristics of the DFT (which you should consider and keep in mind before blindly applying it to your data).
1.The DFT is linear.
2.The DFT is periodic, with a period of N.
3.The IDFT is also periodic!
4. If we consider a shifted signal which happens to fall outside of our defined range, we can use the periodicity property.
4. Evaluating the Fourier Transform in Matlab
Matlab has a very handy built in fft “Fast Fourier Transform” function built in. However, if you are here, you may have tried to use the function and found you didn’t get the results you expected. The attached code ‘discreteFFT_example.m’ defines 3 examples for performing a Fourier transform in Matlab with the appropriate shifting, phase correction, magnitude, and defining of our \xi variable and with all code commented. The code follows the principles laid out in Gaskill [6]. Please also download ‘genFunc.m’ as well as this is called in the example file.
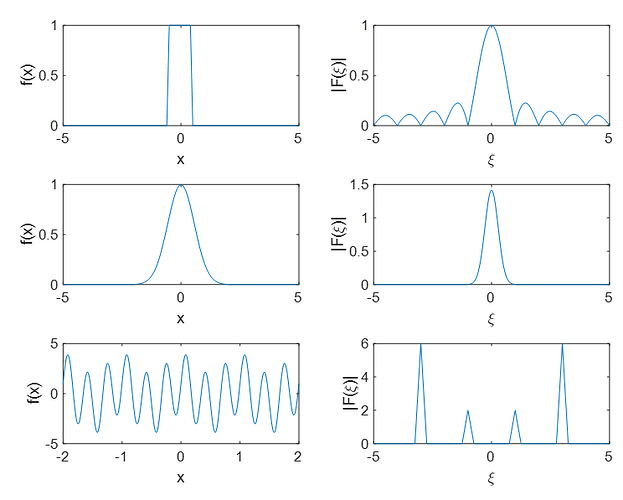
Figure 1. below shows what you can expect to see when running the code:
discreteFFT_example.m:
%% Generate a Basic Function
%This script provides various examples of performing 2d Fourier Transforms
%that can be a guide for how to perform transforms properly on your own
%data sets. The basis for these solutions are from Dr. Gaskill's 'Linear Systems,
%Fourier Transforms, and Optics' as well as Dr. Scott Tyo's Optics 512R
%Course.
%
%
%Author: Logan R. Graves
%
% Version history:
% 12/20/2019 Version 1
% The Terms of Use may be found at the end of this code.
%%
close all
%% Example 1: Rectangle Function
%Define the bounding limit in spatial domain of your function
L=500;
%Create your vector of 'x' points, which are linearly spaced postions that
%your function f(x) will be sampled at.
x=linspace(-L,L,10001);
x=x(1:end-1);
%Define your function, in this case a rect function of width 1.
f=genFunc('rect',x,1,0);
%Define the spacing between your sample points
dx=x(2)-x(1);
%This defines your \xi variable
xi=linspace(0,1/dx,length(x)+1);
xi=xi(1:end-1);
%Calculate the Fourier Transform
F=fft(f);
%Multiply by dx to get the magnitude correct
F = F.*dx;
%Multiply by phase correction factor
F = F.*exp(1i*2*pi*L.*xi);
%Shif the function in the fourier domain of only the real part of the
%function
F=fftshift(abs(F));
%Plot the fourier transformed function against the variable \xi
figure;
title('Fourier Transform of Rect Function');
subplot(3,2,1);
title('Spatial Domain')
plot(x,f);
set(gca,'xlim',[-5,5]);
xlabel('x');
ylabel('f(x)');
subplot(3,2,2);
title('Fourier Domain')
plot([(xi(ceil(end/2)+1:end)-1/dx) xi(1:ceil(end/2))],F);
xlabel('\xi');
ylabel('|F(\xi)|');
%B)
%Define the bounding limit in spatial domain of your function
L=500;
%Create your vector of 'x' points, which are linearly spaced postions that
%your function f(x) will be sampled at.
x=linspace(-L,L,10001);
x=x(1:end-1);
%Define your function, in this case a gaus function of width 1.
f=genFunc('gaus',x,1,0);
%Define the spacing between your sample points
dx=x(2)-x(1);
%This defines your \xi variable
xi=linspace(0,1/dx,length(x)+1);
xi=xi(1:end-1);
%Calculate the Fourier Transform
F=fft(f);
%Multiply by dx to get the magnitude correct
F = F.*dx;
%Multiply by phase correction factor
F = F.*exp(1i*2*pi*L.*xi);
%Shif the function in the fourier domain of only the real part of the
%function
F=fftshift(abs(F));
%Plot the fourier transformed function against the variable \xi
subplot(3,2,3);
title('Spatial Domain')
plot(x,f);
set(gca,'xlim',[-5,5]);
xlabel('x');
ylabel('f(x)');
subplot(3,2,4);
title('Fourier Domain')
plot([(xi(ceil(end/2)+1:end)-1/dx) xi(1:ceil(end/2))],F);
xlabel('\xi');
ylabel('|F(\xi)|');
%c)
%Define the bounding limit in spatial domain of your function
L=2;
%Create your vector of 'x' points, which are linearly spaced postions that
%your function f(x) will be sampled at.
x=linspace(-L,L,10001);
x=x(1:end-1);
%Define your function, in this case a combined sin cos function.
f1=cos(2*pi.*x);
f2=3.*sin(6*pi.*x);
f=f1+f2;
%Define the spacing between your sample points
dx=x(2)-x(1);
%This defines your \xi variable
xi=linspace(0,1/dx,length(x)+1);
xi=xi(1:end-1);
%Calculate the Fourier Transform
F=fft(f);
%Multiply by dx to get the magnitude correct
F = F.*dx;
%Multiply by phase correction factor
F = F.*exp(1i*2*pi*L.*xi);
%Shif the function in the fourier domain of only the real part of the
%function
F=fftshift(abs(F));
%Plot the fourier transformed function against the variable \xi
subplot(3,2,5);
title('Spatial Domain')
plot(x,f);
set(gca,'xlim',[-2,2]);
xlabel('x');
ylabel('f(x)');
subplot(3,2,6);
title('Fourier Domain')
plot([(xi(ceil(end/2)+1:end)-1/dx) xi(1:ceil(end/2))],F);
set(gca,'xlim',[-5,5]);
xlabel('\xi');
ylabel('|F(\xi)|');
genFunc.m :
function output_array=genFunc(funcName, input_array, b, x_0)
%% Generate a Basic Function
%Creates a basic function of a defined width and shifted by a known amount
%using the input array as sample points.
%
%Inputs:
%1) funcName: a string that denotes the function to generate. Can be the
%following:
% 'step': a stepwise function defined as f(x)=0 for x<x_0 and f(x)=1 for
% x>x_0.
% 'tri': a triangle function defined as f(x)=1/(b/2) from [x0 - b/2, x0] and
% f(x) = 1 - 1/(b/2) from [x0, x0 + b/2] and f(x)=0 elsewhere.
% 'rect': a rectangle function defined as f(x)=1 from [x0-b/2, x0+b/2]
% and f(x)=0 elsewhere.
% 'gaus': a gaussian function centered on x0 and with a FWHM of b.
%2) input_array: a 1xN vector of data points over which the Rect func will
%be sampled at.
%3) b: an integer value define the full width of the rectangle.
%4) x_0: a float value defining the shift from center of the rectangle
%function.
%
%Outputs:
%1) output_array: a 1xN vector of data points defining the function
%values sampled at the input_array points.
%
%Author: Logan R. Graves
%
% Version history:
% 08/04/2015 Version 1
% 12/20/2019 Version 2
% The Terms of Use may be found at the end of this code.
%%
%
%% Parse variables
if nargin < 2
println("You did not input sufficient variables. Please try again.");
exit
elseif nargin < 3
b = 1;
x0 = 0;
elseif nargin < 4
x0 = 0;
end
%% Parse text input
switch funcName
case "step"
output_array = stepFunc(input_array, x_0);
case "tri"
output_array = triFunc(input_array, b, x_0);
case "rect"
output_array = rectFunc(input_array, b, x_0);
case "gaus"
output_array = gausFunc(input_array, b, x_0);
otherwise
output_array = zeros(length(input_array));
println("The func type is not recognized. The recongized commands are [step], [tri], [rect]");
end
end
function outFunc = stepFunc(input_array, x0)
%initialize the output to be a vector of zeros of the same size as the input
outFunc = zeros(size(input_array));
% Input Array
input_array = input_array - x0;
%define all values for input array >0 as 1.
outFunc(find(input_array>=0))=ones(size(find(input_array>=0)));
end
function outFunc = triFunc(input_array, b, x0)
%initialize the output to be a vector of zeros of the same size as the input
outFunc = zeros(size(input_array));
% Determine triangle limits
startEdge = x0 - b/2;
endEdge = x0 + b/2;
midPoint = x0;
%Determine slope of triangle
slope = 2/b;
%define all values for input array >0 as 1.
for arrayPos = 1:length(input_array)
%Determine current x value
xVal = input_array(arrayPos);
%Check which part of the piecewise function applies
if xVal < startEdge || xVal >= endEdge
outFunc(arrayPos) = 0;
elseif xVal >= startEdge && xVal < midPoint
outFunc(arrayPos) = 1 + (xVal-x0)*slope;
elseif xVal >= midPoint && xVal < endEdge
outFunc(arrayPos) = 1 + (xVal-x0)*-slope;
end
end
end
function outFunc = rectFunc(input_array, b, x0)
%initialize the output to be a vector of zeros of the same size as the input
outFunc = zeros(size(input_array));
% Determine triangle limits
startEdge = x0 - b/2;
endEdge = x0 + b/2;
midPoint = x0;
%define all values for input array >0 as 1.
for arrayPos = 1:length(input_array)
%Determine current x value
xVal = input_array(arrayPos);
%Check which part of the piecewise function applies
if xVal < startEdge || xVal >= endEdge
outFunc(arrayPos) = 0;
elseif xVal >= startEdge && xVal < midPoint
outFunc(arrayPos) = 1 ;
elseif xVal >= midPoint && xVal < endEdge
outFunc(arrayPos) = 1 ;
end
end
end
function outFunc = gausFunc(input_array, b, x0)
%initialize the output to be a vector of zeros of the same size as the input
outFunc = exp(-pi.*((input_array-x0).^2)./(2*b^2));
end
Evaluating Fourier Transform in Julia
coming soon…
References
[1]OPTI512R - Linear Systems and Fourier Optics on Apple Podcasts
[2]Fourier Series -- from Wolfram MathWorld
[3]http://www.thefouriertransform.com
[4]https://marksmannet.com/RobertMarks/REPRINTS/1999_IntroductionToShannonSamplingAndInterpolationTheory.pdf
[5]https://www.unirioja.es/cu/jvarona/downloads/Dunkl-Sampling.pdf
[6]Gaskill, J.D., and John Wiley \& Sons. Linear Systems, Fourier Transforms, and Optics. Wiley Series in Pure and Applied Optics. Wiley, 1978.